\begin{aligned} \dfrac{d}{dx}\sin(x) =\,&\, \lim \limits_{\Delta x\to 0} \dfrac{\sin(x+\Delta x)-\sin(x)}{\Delta x} \\ =\,&\, \lim \limits_{\Delta x\to 0} \dfrac{\sin(x)\cos(\Delta x)+\sin(\Delta x)\cos(x)-\sin(x)}{\Delta x} \\ =\,&\, \lim \limits_{\Delta x\to 0} \left[\cos(x)\dfrac{\sin(\Delta x)}{\Delta x} - \sin(x)\dfrac{1-\cos(\Delta x)}{\Delta x} \right] \\ =\,&\, \cos(x)\lim \limits_{\Delta x\to 0}\dfrac{\sin(\Delta x)}{\Delta x} - \sin(x)\lim \limits_{\Delta x\to 0}\dfrac{1-\cos(\Delta x)}{\Delta x} \\ =\,&\, \cos(x)(1) - \sin(x)(0) \\ =\,&\, \cos(x) \end{aligned}

\begin{aligned} \dfrac{d}{dx}\cos(x) =\,&\, \lim \limits_{\Delta x\to 0} \dfrac{\cos(x+\Delta x)-\cos(x)}{\Delta x} \\ =\,&\, \lim \limits_{\Delta x\to 0} \dfrac{\cos(x)\cos(\Delta x)-\sin(\Delta x)\sin(x)-\cos(x)}{\Delta x} \\ =\,&\, \lim \limits_{\Delta x\to 0} \left[-\sin(x)\dfrac{\sin(\Delta x)}{\Delta x} - \cos(x)\dfrac{1-\cos(\Delta x)}{\Delta x} \right] \\ =\,&\, -\sin(x)\lim \limits_{\Delta x\to 0}\dfrac{\sin(\Delta x)}{\Delta x} - \cos(x)\lim \limits_{\Delta x\to 0}\dfrac{1-\cos(\Delta x)}{\Delta x} \\ =\,&\, -\sin(x)(1) - \cos(x)(0) \\ =\,&\, -\sin(x) \end{aligned}

\begin{aligned} \dfrac{d}{dx}\tan(x) =\,&\, \dfrac{d}{dx}\left[\dfrac{\sin(x)}{\cos(x)}\right] \\ =\,&\, \dfrac{\cos(x)\dfrac{d}{dx}\sin(x)-\sin(x)\dfrac{d}{dx}\cos(x)}{\cos^2(x)} \\ =\,&\, \dfrac{\cos(x)\cos(x)+\sin(x)\sin(x)}{\cos^2(x)} \\ =\,&\, \dfrac{\cos^2(x)+\sin^2(x)}{\cos^2(x)} \\ =\,&\, \dfrac{1}{\cos^2(x)} = \sec^2(x) \end{aligned}

\begin{aligned} \dfrac{d}{dx}\cot(x) =\,&\, \dfrac{d}{dx}\left[\dfrac{\cos(x)}{\sin(x)}\right] \\ =\,&\, \dfrac{\sin(x)\dfrac{d}{dx}\cos(x)-\cos(x)\dfrac{d}{dx}\sin(x)}{\sin^2(x)} \\ =\,&\, \dfrac{-\sin(x)\sin(x)-\cos(x)\cos(x)}{\sin^2(x)} \\ =\,&\, \dfrac{-\left[\sin^2(x)+\cos^2(x)\right]}{\sin^2(x)} \\ =\,&\, \dfrac{-1}{\sin^2(x)} = -\csc^2(x) \end{aligned}

\begin{aligned} \dfrac{d}{dx}\sec(x) =\,&\, \dfrac{d}{dx}\left[\dfrac{1}{\cos(x)}\right] \\ =\,&\, \dfrac{\cos(x)\dfrac{d}{dx}(1)-(1)\dfrac{d}{dx}\cos(x)}{\cos^2(x)} \\ =\,&\, \dfrac{\cos(x)(0)+(1)\sin(x)}{\cos^2(x)} \\ =\,&\, \dfrac{\sin(x)}{\cos^2(x)} = \dfrac{1}{\cos(x)}\dfrac{\sin(x)}{\cos(x)}\\ =\,&\, \sec(x)\tan(x) \end{aligned}

\begin{aligned} \dfrac{d}{dx}\csc(x) =\,&\, \dfrac{d}{dx}\left[\dfrac{1}{\sin(x)}\right] \\ =\,&\, \dfrac{\sin(x)\dfrac{d}{dx}(1)-(1)\dfrac{d}{dx}\sin(x)}{\sin^2(x)} \\ =\,&\, \dfrac{\sin(x)(0)-(1)\cos(x)}{\sin^2(x)} \\ =\,&\, \dfrac{-\cos(x)}{\sin^2(x)} = \dfrac{-1}{\sin(x)}\dfrac{\cos(x)}{\sin(x)}\\ =\,&\, -\csc(x)\cot(x) \end{aligned}

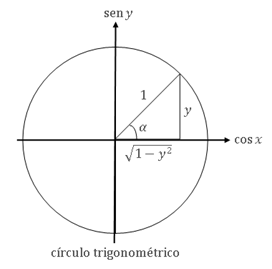Derivada da função arco-seno Da figura ao lado temos \( y=\sin\alpha \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \alpha=\sin^{-1}y \hspace{0.4cm}\text{ e }\hspace{0.4cm} \cos\alpha=\sqrt{1-y^2}\) Então, \begin{aligned} y =\,&\, \sin\alpha \\ \dfrac{d}{dy}y =\,&\, \dfrac{d}{dy}\sin\alpha \\ 1 =\,&\, \cos\alpha\dfrac{d}{dy}\alpha = \sqrt{1-y^2}\,\dfrac{d}{dy}\sin^{-1}y\\ \dfrac{d}{dy}\sin^{-1}y =\,&\, \dfrac{1}{\sqrt{1-y^2}} \hspace{0.4cm}\text{ ou }\hspace{0.4cm} \dfrac{d}{du}\sin^{-1}(u)=\dfrac{1}{\sqrt{1-u^2}} \end{aligned}

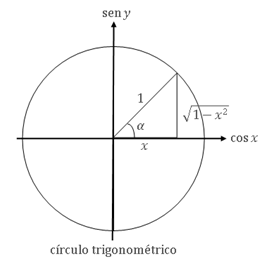Derivada da função arco-cosseno Da figura ao lado temos \( x=\cos\alpha \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \alpha=\cos^{-1}x \hspace{0.4cm}\text{ e }\hspace{0.4cm} \sin\alpha=\sqrt{1-x^2}\) Então, \begin{aligned} x =\,&\, \cos\alpha \\ \dfrac{d}{dx}x =\,&\, \dfrac{d}{dx}\cos\alpha \\ 1 =\,&\, -\sin\alpha\dfrac{d}{dx}\alpha = -\sqrt{1-x^2}\,\dfrac{d}{dx}\cos^{-1}x\\ \dfrac{d}{dx}\cos^{-1}x =\,&\, -\dfrac{1}{\sqrt{1-x^2}} \hspace{0.4cm}\text{ ou }\hspace{0.4cm} \dfrac{d}{du}\cos^{-1}(u)=-\dfrac{1}{\sqrt{1-u^2}} \end{aligned}

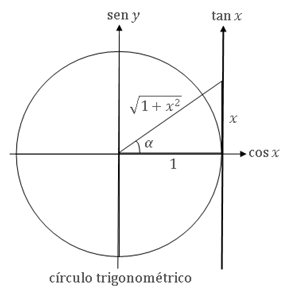Derivada da função arco-tangente Da figura ao lado temos \( x=\tan\alpha \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \alpha=\tan^{-1}x \hspace{0.4cm}\text{ e }\hspace{0.4cm} \cos\alpha=\dfrac{1}{\sqrt{1+x^2}} \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \cos^2\alpha=\dfrac{1}{1+x^2} \) Então, \begin{aligned} x =\,&\, \tan\alpha \\ \dfrac{d}{dx}x =\,&\, \dfrac{d}{dx}\tan\alpha \\ 1 =\,&\, \sec^2\alpha\,\dfrac{d}{dx}\alpha = (1+x^2)\,\dfrac{d}{dx}\tan^{-1}x\\ \dfrac{d}{dx}\tan^{-1}x =\,&\, \dfrac{1}{1+x^2} \hspace{0.4cm}\text{ ou }\hspace{0.4cm} \dfrac{d}{du}\tan^{-1}(u)=\dfrac{1}{1+u^2} \end{aligned}

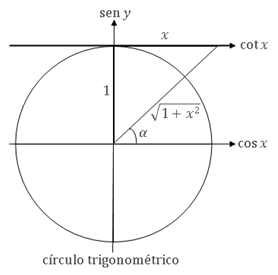Derivada da função arco-cotangente Da figura ao lado temos \( x=\cot\alpha \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \alpha=\cot^{-1}x \hspace{0.4cm}\text{ e }\hspace{0.4cm} \sin\alpha=\dfrac{1}{\sqrt{1+x^2}} \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \sin^2\alpha=\dfrac{1}{1+x^2} \) Então, \begin{aligned} x =\,&\, \cot\alpha \\ \dfrac{d}{dx}x =\,&\, \dfrac{d}{dx}\cot\alpha \\ 1 =\,&\, -\csc^2\alpha\,\dfrac{d}{dx}\alpha = -(1+x^2)\,\dfrac{d}{dx}\cot^{-1}x\\ \dfrac{d}{dx}\cot^{-1}x =\,&\, -\dfrac{1}{1+x^2} \hspace{0.4cm}\text{ ou }\hspace{0.4cm} \dfrac{d}{du}\cot^{-1}(u)=-\dfrac{1}{1+u^2} \end{aligned}

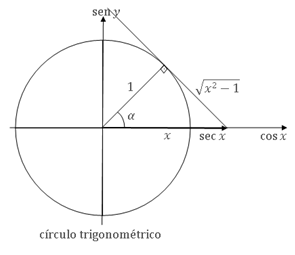Derivada da função arco-secante Da figura ao lado temos \( \cos\alpha=\dfrac{1}{x} \hspace{0.4cm}\Rightarrow\hspace{0.4cm} x=\dfrac{1}{\cos\alpha}\equiv\sec\alpha \) \( x=\sec\alpha \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \alpha=\sec^{-1}x \hspace{0.4cm}\text{ e }\hspace{0.4cm} \tan\alpha=\sqrt{x^2-1} \) Então, \begin{aligned} x =\,&\, \sec\alpha \\ \dfrac{d}{dx}x =\,&\, \dfrac{d}{dx}\sec\alpha \\ 1 =\,&\, \sec\alpha\tan\alpha\,\dfrac{d}{dx}\alpha = x\,\sqrt{x^2-1}\,\dfrac{d}{dx}\sec^{-1}x\\ \dfrac{d}{dx}\sec^{-1}x =\,&\, \dfrac{1}{x\,\sqrt{x^2-1}} \hspace{0.4cm}\text{ ou }\hspace{0.4cm} \dfrac{d}{du}\sec^{-1}(u)=\dfrac{1}{|u|\sqrt{u^2-1}} \end{aligned}

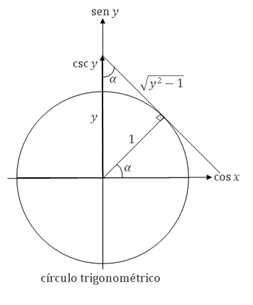Derivada da função arco-cossecante Da figura ao lado temos \( \sin\alpha=\dfrac{1}{y} \hspace{0.4cm}\Rightarrow\hspace{0.4cm} y=\dfrac{1}{\sin\alpha}\equiv\csc\alpha \) \( y=\csc\alpha \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \alpha=\csc^{-1}y \hspace{0.4cm}\text{ e }\hspace{0.4cm} \cot\alpha=\sqrt{y^2-1} \) Então, \begin{aligned} y =\,&\, \csc\alpha \\ \dfrac{d}{dy}y =\,&\, \dfrac{d}{dy}\csc\alpha \\ 1 =\,&\, -\csc\alpha\cot\alpha\,\dfrac{d}{dy}\alpha = -y\,\sqrt{y^2-1}\,\dfrac{d}{dy}\csc^{-1}y\\ \dfrac{d}{dy}\csc^{-1}y =\,&\, -\dfrac{1}{y\,\sqrt{y^2-1}} \hspace{0.4cm}\text{ ou }\hspace{0.4cm} \dfrac{d}{du}\csc^{-1}(u)=-\dfrac{1}{|u|\sqrt{u^2-1}} \end{aligned}

Da definição temos: \( n\,!=n\cdot(n-1)\,! \quad\longrightarrow\quad \) Se \(\hspace{0.4cm} n = 1 \) Então, \begin{aligned} 1\,!=\,&\, 1\cdot(1-1)\,! \\ 1\,=\,&\, 1\cdot 0\,! \\ 0\,!=\,&\, 1 \hspace{2cm} \blacksquare \end{aligned}